What Is Zero Divided by Zero? - The Actual Fact
Division by zero means a division where the divisor i.e. denominator is zero. Considering the dividend (numerator) as a...
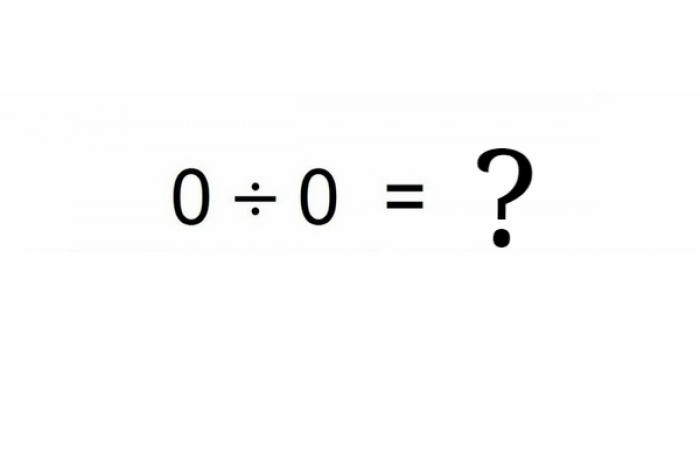
Division by zero means a division where the divisor i.e. denominator is zero. Considering the dividend (numerator) as a where a is not equal to 0, this division can be expressed as a/0. This expression has no meaning in ordinary arithmetic since there is no number which can be multiplied by 0 and so division by 0 is undefined. One of the earliest recorded references to this mathematical impossibility is contained in George Berkeley's criticism of infinitesimal calculus in The Analyst.
Taking all this in simpler terms, division is considered as splitting a set of objects in equal parts. If ten cookies are to be divided equally among five people, then each one would receive 10/5 = 2 cookies. But what if we want to divide 10 cookies among 0 people? In mathematical jargon, 10 items cannot be partitioned into 0 subsets. So, 10/0 in elementary arithmetic is meaningless or undefined.
But have you thought what the result of 0 divided by 0 is? Let’s find out.
Consider three arbitrary real number x, y and z.
If x/y = z, then x = y * z
(assuming y is not equal to 0)
But if x and y = 0 then
0 = 0 * z
This means that z can either be 0, 42 or even under root (-1) and so on. This concludes that 0/0 is undefined.
0/0 is not only undefined but also an indeterminate form. Moreover, it means that you have made a mistake in the formulation. You need to reconsider the question.
Exceptions:-
However, there are some mathematical structures in which a/0 is defined such as in Riemann sphere and the projectively extended real line. But these structures cannot satisfy every ordinary rule of arithmetic.
There are some other contexts where division by zero can be considered as defined.
For 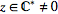 in extended complex plane C-*, z/0 is a quantity known as complex infinity.
in extended complex plane C-*, z/0 is a quantity known as complex infinity.
Although division by zero is not defined for real numbers, limits that involve division by a real quantity x which approaches zero can be defined. For example,
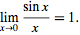
But some limits may also approach infinity,
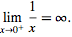
Popular Posts
What Is Trypophobia – A Disgust More Than Fear
"I can't really face small, irregularly or asymmetrically placed holes, they make me like, throw up in my mouth, cry a little bi...
Chandan Roy
16 Interesting Facts About Ambidextrous People
A lefty or left-handed uses his left hand more naturally and dominantly than the right hand. And the righty or right-handed is o...
Ethan Stephans
20 Interesting Facts About Meteoroid, Meteor and Meteorite
Watching celestial objects is a true delight. It is still fun to catch a sight of shooting stars when we grow up. A second of th...
Swati Bhandari








